被诈骗了,老师一直强调不会让我们写所有代码,说是代码填空。
结果是全部要手写
算法的定义
算法是求解问题的一系列计算步骤,用来将输入转换成输出结果
时间复杂性是指执行算法所需要的时间资源
空间复杂性是指执行算法所需要的空间资源
关于算法的复杂度
算法所耗费的时间应是算法中每条语句的执行时间之和,而每条语句的执行
时间就是该语句的执行次数(频度)与该语句执行一次所需时间的乘积
渐进符号
O(渐进上界)
用来描述增长率的上限,当输入规模为n时,算法消耗时间的最大
这个上限的阶越低,结果就越有价值。
Ω(渐进下界)
用来描述增长率的下限,当输入规模为n时,算法消耗时间的最小,
这个下限的阶越高,结果就越有价值。
θ(同阶符号)
若上界和下界同阶,那么可以使用这个符号,也可以是精确阶。
若时间复杂度为 $T(n)$,那么 $T(n)$ 就是精确阶,即 $θ(n)=T(n)$
若上下界相等,那么也有 $θ(n)=O(n)=Ω(n)$
计算渐进阶
设算法的时间复杂性为 $T(n)$
若 $T(n)=5n^2+8n+1$
则 $5n^2+8n+1<=5n^2+8n+n=5n^2+9n<=5n^2+9n^2=14n^2=O(n^2)$
则 $5n^2+8n+1>=5n^2=Ω(n^2)$
则 $θ(n)=T(n)$
Master定理(主定理)
$T(n)=a*T(n/b)+f(n)$
对于 $T(n)=2T(3n/2)$ 来说,其中 $b=2/3$
时间复杂度为 $n^{log_b^a}$ 和 $f(n)$ 中的较大值
如果相等,那就取 $f(n)logn$
利用主定理求下列递归方程的时间复杂度:
$T(n)=5T(n/2)+\theta(n^2)$
$a=5,b=2,f(n)=n^2$
$n^{log_b^a}=n^{log_2^5}>f(n)$
$\therefore T(n)=\theta(n^{log_2^5})$
$T(n)=2T(n/2)+n$
$a=2,b=2,f(n)=n$
$n^{log_b^a}=n=f(n)$
$\therefore T(n)=\theta(nlogn)$
$T(n)=5T(n/2)+\theta(n^3)$
$a=5,b=2,f(n)=n^3$
$n^{log_b^a}=n^{log_2^5}<f(n)$
$\therefore T(n)=\theta(n^3)$
分治法的基本思想(能解决的问题拥有的特征)
最优子结构性质:该问题可以分解为若干个规模较小的相同问题。
利用该问题分解出的子问题的解可以合并为该问题的解。
该问题所分解出的子问题之间相互独立,即子问题之间不包含公共的子问题。
归并排序和快速排序采用的是什么策略
分治策略
棋盘覆盖问题-查看学习题作业2-2023.9.27
动态规划算法的两个要素,计算的基本步骤
最优子问题性质
重叠子问题性质
计算的基本步骤
1、找出最优解的性质,并刻画其结构特征。
2、递归地定义最优值。
3、以自底向上的方式计算出最优值。
4、根据计算最优值时得到的信息,构造最优解
矩阵连乘 $A_{1}A_{2}A_{3}A_{4}A_{5}$ 的5种加括号方式
$A_{1}A_{2}$ 先相乘
1.和 $A_{3}A_{4}$ 相乘
2.$A_{3}$ 和 $A_{4}$ 先相乘,再乘
$(((A_{1}A_{2})A_{3})A_{4})$
$((A_{1}A_{2})(A_{3}A_{4}))$
$A_{2}A_{3}$ 先相乘
3.先和 $A_{1}$ 乘
4.先和 $A_{4}$ 乘
$((A_{1}(A_{2}A_{3}))A_{4})$
$(A_{1}((A_{2}A_{3})A_{4}))$
$A_{3}A_{4}$ 先相乘
5.再乘前面的
$(A_{1}(A_{2}(A_{3}A_{4})))$
备忘录方法和dp方法的不同之处
动态规划算法是备忘录方法的变形,它通过分治思想对原问题进行分解,以存储子问题的解
的方式解决冗余计算,并采用自底向上的递推方式获取问题的最终解。
递推方式是自底向上递归求解,而备忘录方法是自顶向下递归求解。当一个问题的所有子问题
都至少解一次时,可以考虑使用动态规划算法。当子问题空间中的部分子问题不需要求解时,
可以考虑备忘录方法。
01背包可以用哪些方法解决
回溯
分支限界
动态规划
动态规划解决最大子段和的复杂度
时间复杂度 $O(n)$
空间复杂度 $O(n)$
凸多边形最优三角剖分问题用什么方法解决
动态规划
活动安排问题的选择贪心策略
按照一定的顺序安排活动,使得进行尽可能多的活动。
(1)最早开始时间,这样可以增大资源的利用率
(2)最早结束时间,这一可以使下一个活动尽早开始
哈夫曼树是用什么算法构造的
贪心算法
背包问题和01背包问题哪个可以用贪心
(完全)背包问题可以用贪心算法
01背包不行
回溯法的两种典型解空间树
子集树(n个元素中找出某个子集解决问题),排列树(要求n个元素是满足某种排列的问题)
其中符号三角形问题是子集树
01背包也是子集树
旅行商问题是排列树
分支限界法根据选择扩展节点分为哪两类
队列式分支限界法
优先队列式分治限界法
队列式分支限界法的框架
(1)初始化解空间树的根结点(第一个活结点)和一个空队列。
(2)根结点入队列
(3)若队列不为空,则循环执行以下各步
出队一个结点P(当前扩展结点)
while(P的所有满足约束条件的孩子结点T)
{
若T不是叶子结点
则将T加入队列
否则用于更新最优值及记录该叶子结点
}
(4)根据记录的叶子结点构造最优解
优先队列式分支限界法的框架
(1)初始化解空间树的根结点(当前扩展结点)P和一个空堆
(2)while(当前扩展结点P不是叶子结点)
{
while(P的所有满足约束条件的孩子结点T)
{
将T插入堆
}
堆顶元素赋值给P;
}
(3)根据当前扩展结点P求最优值并构造最优解
优先队列每个节点只有几次机会成为扩展节点(分治限界法)
一次
旅行商在分支限界法中用优先队列用的是最大堆还是最小堆
最小堆
最大团问题
最大团代码(有修改的高分代码,无原题,有相同题)
若某个图中的一个子图满足任意两个节点可以互相到达
那么这个子图就是一个团
最大团就是取其中节点数最多的那个满足条件的子图
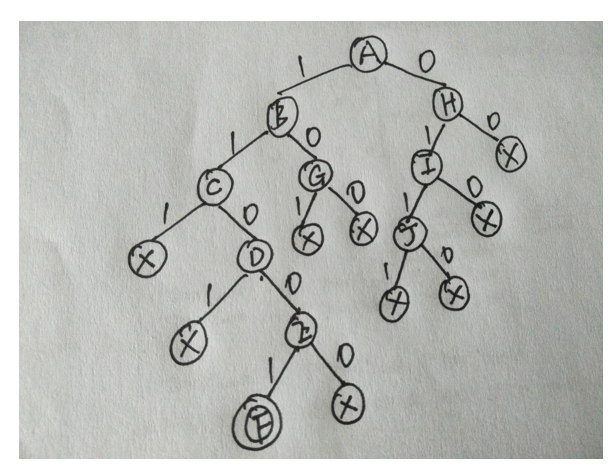
考虑使用子集树解决问题,假设有节点A,B,C,D,E,F(每个节点只存在用或者不用的情况,构造解空间)
A节点为根节点,往左写1代表使用A节点,往右写0代表不使用A节点
如果某个节点选入不能满足团问题,那么打上一个叉,如果最后的叶子节点满足条件,那么圈起来。

分治找最大元素
int max(int A[],int low,int high){
if(low==high){
return A[low];
}
int mid=(low+high)/2;
int a=max(A,low,mid);
int b=max(A,mid+1,high);
if(a大于b){
return a;
}else return b;
}
分治找最小元素
int min(int A[],int low,int high){
if(low==high){
return A[low];
}
int mid=(low+high)/2;
int a=min(A,low,mid);
int b=min(A,mid+1,high);
if(a小于b){
return a;
}else return b;
}
分治找大于x的元素
void com(int A[], int low, int high, int x) {
if (low == high) {
if (A[low] > x) {
cout << A[low] << endl;
}
} else {
int mid = (low + high) / 2;
com(A, low, mid, x);
com(A, mid + 1, high, x);
}
}
最长公共子序列图表法
如果当前位置相等,那么画一个左上箭头,值为从上面+1或者左边+1的较大值
如果不相等,那么为0,或者左箭头继承,或者上箭头继承,取较大值
行列推进:即第一行对完,对第一列,再第二行,再第二列。其中行和列哪个先没关系。
详细看下面样例
BDCABA和ABCBDAB的最长公共子序列图表法
B D C A B A
A
B
C
B
D
A
B
->
B D C A B A
A 0 0 0 1↖ 1← 1↖
B 1↖
C 1↑
B 1↖
D 1↑
A 1↑
B 1↖
->后面的类推
https://test-6gmfrj63dcea73d7-1321055059.tcloudbaseapp.com/2023/12/30/%E7%AE%97%E6%B3%95%E6%9C%9F%E6%9C%AB/
答案在这里面自行校对
活动安排问题的sort代码
void sort(int s[],int f[],int n){
//把各个活动的起始时间和结束时间按结束时间非降序排序(即升序,但是可以相等)
int a,b;
int i,j;
//相当于从j中选出最早的放到i处
for(i=0;i小于n;i++){
for(j=i+1;j小于n;j++){
if(f[i]大于f[j]){
a=f[i]; f[i]=f[j]; f[j]=a; //交换f[i]和f[j]
b=s[i]; s[i]=s[j]; s[j]=b; //交换s[i]和s[j]
}
}
}
}
活动安排问题的贪心代码
int actionmanage(int s[],int f[],bool a[],int n){
//把各个活动的起始时间和结束时间按结束时间非降序排序,s和f已经排序了
a[0]=1;//最早活动0选上
int i;
int j=0,count=1;//下一个活动的开始在前一个活动的之后才能选
for(i=1;i小于n;i++){
if(s[i]大于等于f[j]){//下一个活动可以选,就选上
a[i]=1;
j=i;
count++;
}
else a[i]=0;//不能选就不要
}
return count;
}
最优装载问题代码
装尽可能多的货物,所以从小到大排序重量,从小到大开始选上(太简单就不放代码)